ご無沙汰、ご無沙汰。
約2週間ぶりの投稿となります。入学や引っ越しの手続きに追われていつの間にか新年度になっていた次第であります。時が経つのは早いな〜（すっとぼけ）
数学と物理のどちらか一方が苦手、もしくは微積物理を学びたいと思っている方むけにこの記事を書かさせていただきます。
どっちも苦手だよー、という人むけにも絶賛記事作成中ですので今しばらくお持ちください！
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
この記事は
- 数学はできるんだけど物理がちょっと、という人
- その逆の人
- 微積物理を学びたいんだよ、という人
向けです。
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
今日は大学受験における数学と物理の関係についてお話しします。数学Ⅲで学ぶ微分積分の知識を活かして物理を解く、そして物理の公式の意味を数学の力を活かして読み解いていく、そういったことまでできると物理がますます面白くなるかも知れません。さらに、等加速度運動の公式の導出を通して微積物理を少しだけ体験してみましょう！
そして最後には京都大学に現役合格した筆者が使っていた数学と物理の参考書を教えちゃいます！
簡潔に微分積分とは？
微分積分とは17世紀から18世紀にかけてかの有名なニュートンやライプニッツ達によって確立されていった学問です。簡単に微分積分を表現してみます。あくまで”簡単に”です。
微分
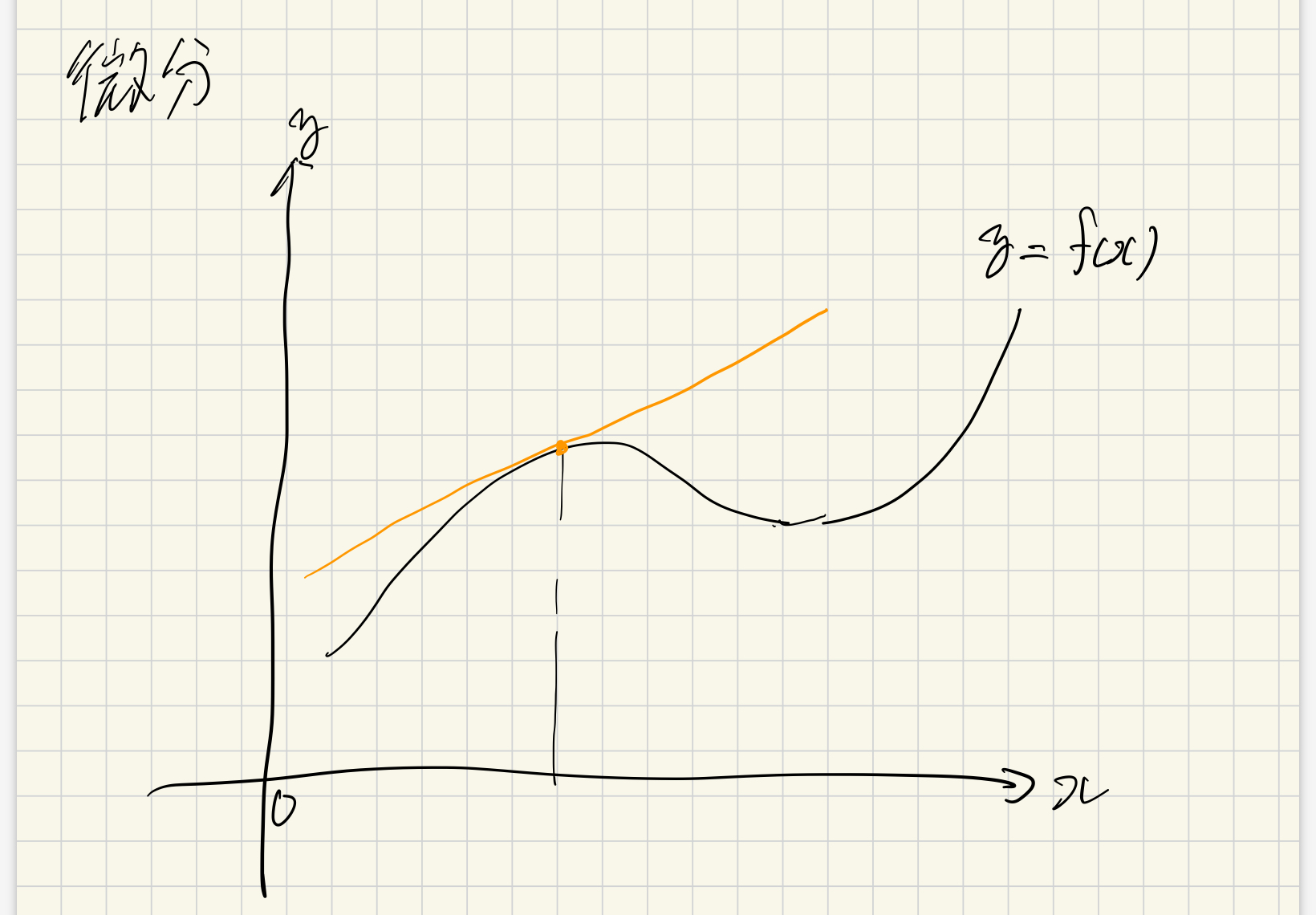
超大雑把にいうとあるグラフにおいてある点での傾きで
例えば y＝（距離）x＝（時間）であれば橙色の線の傾きはその時間での瞬間の速さを意味するわけです。
積分
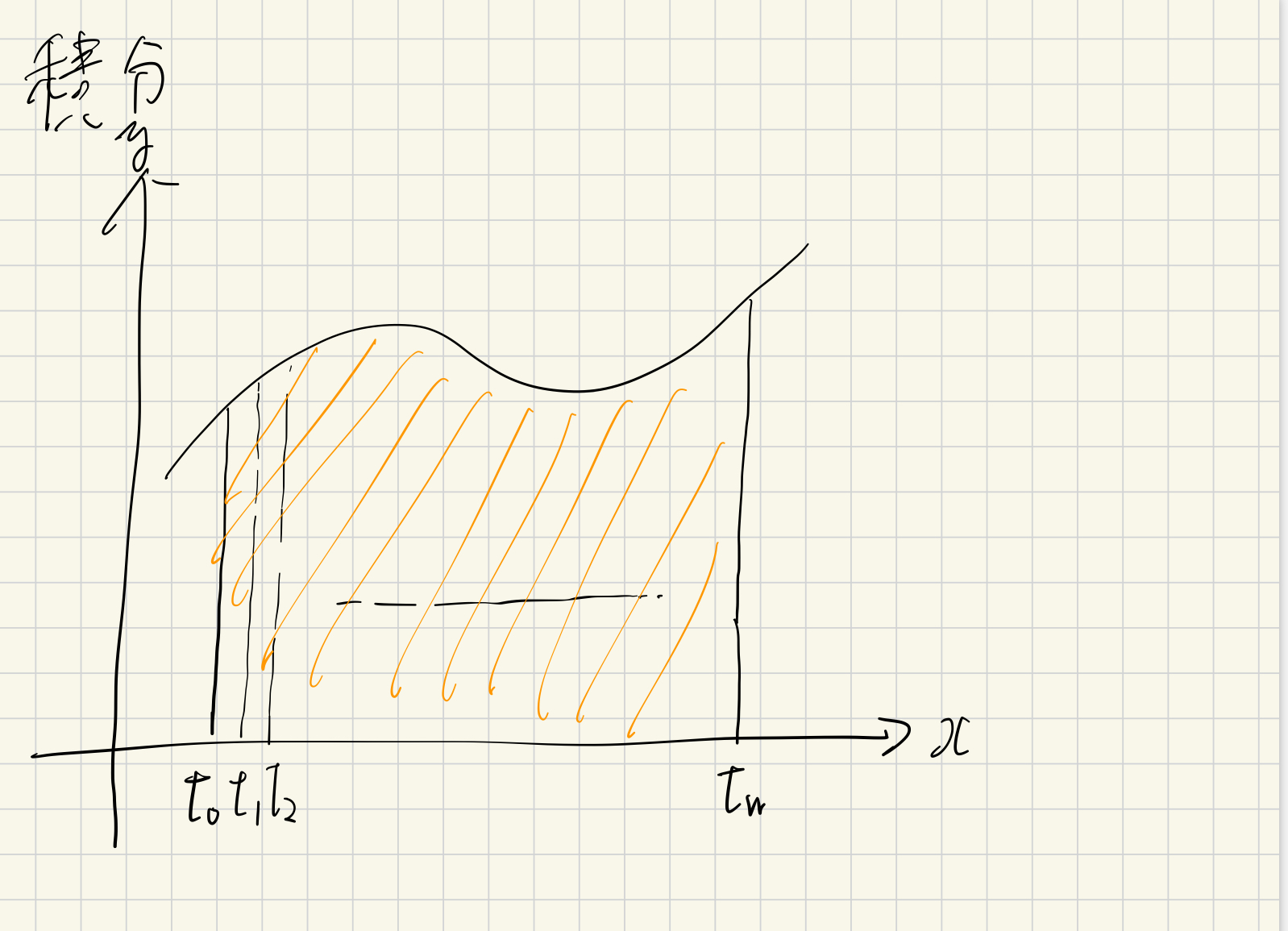
これまた超大雑把に説明すると積分によって橙色の部分の面積を素麺のように細い長方形で切り分けてそれをそれぞれ足し合わせることによって求めることができます。
例えば y＝（速さ）,x＝（時間）とすると橙色の面積はt(0)→t(n)の間に橙色の面積分だけ移動したことになります。
等加速度運動の公式を導出してみよう！
大体な説明でも感覚だけわかれば等加速度運動の公式を導出することが可能です！それではやってみましょう。
まず（加速度）＝ a （＝定数）,初速Vとしておきます。
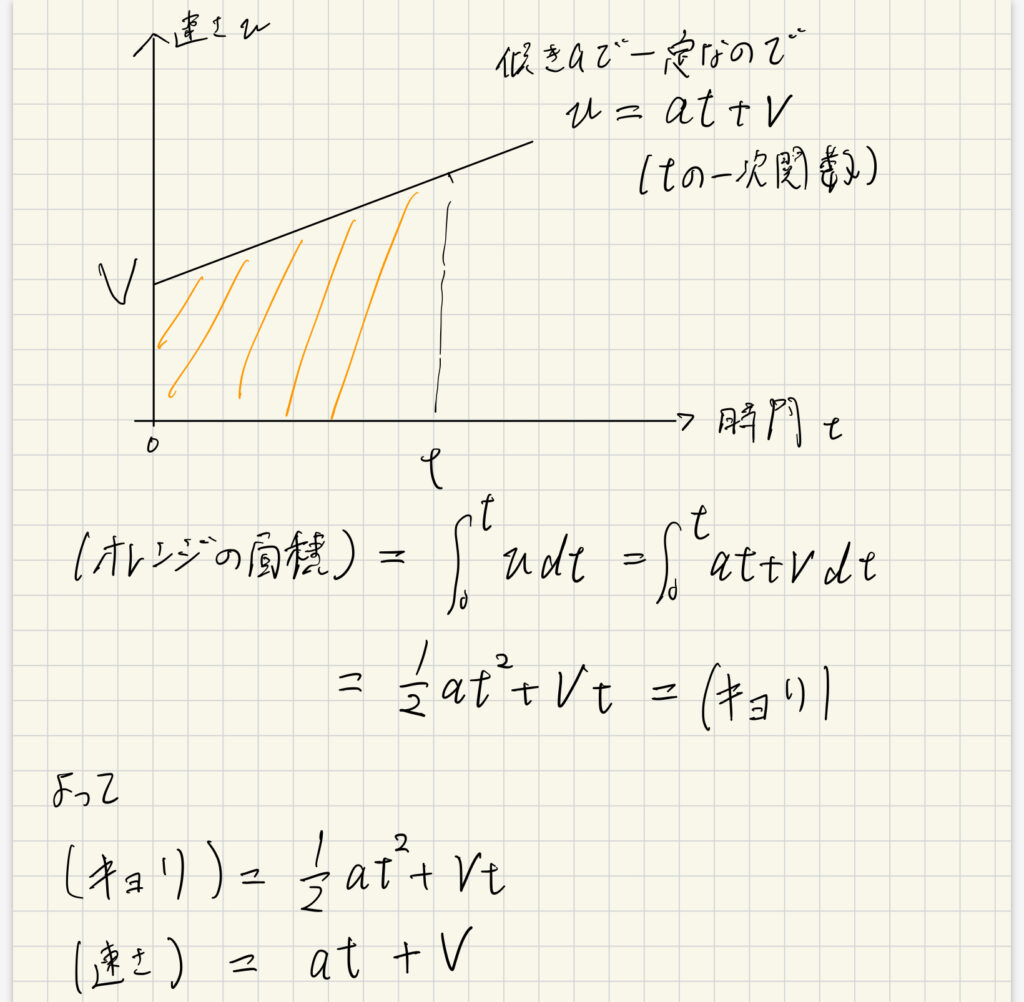
物理を本業としてる人が見たら疑問を抱く点も多々あると思いますが、簡単に微積物理の例えとして等加速度運動の公式が導けました。
こんなもんじゃなくてもっとガチの大学の物理をやりたいんだという人におすすめの書籍を紹介しておきます。
基幹講座 物理学 力学 東京図書 篠本 滋 (著), 坂口 英継 (著), 益川 敏英 (監修), 植松 恒夫 (編集), 青山 秀明 (編集)
高校３年の時に買って電車の中で読みました。しっかり理解することは実力不足でできなかったけど感覚を養うことができました。感覚というものは大事です。何かと頼りになります。高校数学ができれば取り組めるのでもし時間に余裕のある人は見てみてもいいかも知れません。
（Amazonリンク予定地）
おすすめ参考書５選＋１
筆者が実際に受験生の時に使っていた参考書を紹介します！
この参考書達で感覚を養って合格を勝ち取れたといっても過言ではないです。
どうせ青チャートでも勧めてくるんだろ！というそこのあなた！！（筆者は赤チャートを愛用していました。赤と青では例題はそこまで難易度の差はないのですが赤チャートの章末問題はなかなか歯応えがあって取り組みづらい印象があります。マニアックな参考書が今日のテーマなのでチャート式の話はここらへんにしておきます。）
一応リンク貼っちゃお
（チャート式 Amazonリンク予定地）
あえてそこまで有名じゃないものを取り上げてみました！
あなたにこそ伝えたい参考書を５冊！
テーマ別演習① 入試数学の掌握 総論編 Yell books 著 近藤至徳
早速受験数学熱をくすぐる名著から紹介します！受験の熱意に満ち溢れている人ならもしかしたら巷で聞いたことがあるかも知れません。タイトルがいいですよね。入試数学を全て手の内に入れてしまう、そうすると、出題者の意図まで読めてしまう、問題に付属する条件が及ぼす影響まで読めてしまう、ロマン溢れる一冊でございます。（軍艦で例えると戦艦「金剛」ぐらい）数学の感覚を体験することができます！
筆者の感想
高校2年の夏休みと高校3年の１０月頃に使用していました。読者の方に注意喚起しておくのですが、間違っても高校の2年の時期にましてや夏休みに使用すべきではない、少なくともすべきではなかったです。（特段に数学が大好きであったり、中高一貫校で授業のペースが早い人はもしかすると取り組んでもいいかも）しかしながら、早い時期に取り組んでみて、受験数学とは、数学の難問題の構成とは、と言うものを早いうちから知れたのはよかった点だと感じました。
何よりも、めっちゃやる気出る
これに尽きます。
ぜひ皆様も一度手に取ってみてください！
（Amazonのリンク予定地）
数学Ⅰ＋A＋Ⅱ＋B＋ベクトル 上級問題精講 旺文社 著 長崎憲一
上級問題精講には数学Ⅲ＋Cの本も販売されているのですが、私は断念しました。（難しすぎるって！チェビシェフ多項式の証明とかでけへんて！）しかしながら、数学Ⅰ＋A＋Ⅱ＋B＋ベクトル 上級問題精講の方にはお世話になりました。入試数学の掌握で学ばせてもらったことを反映することができ、この組み合わせで、大きく成長することができたと思います。
筆者の感想
私は入試数学の掌握を一通り終えた後にこの参考書を取り組み始めました。つまり、１１月ごろになりますかね。京都大学の過去問と似た問題を選りすぐって解き進めました。その時期になると取捨選択も重要になるかと思います。全ての数学の分野（確率とか不等式とか微積とか）の問題が揃っていたのでとても使いやすかったです。
青いやつです！
ぜひご覧あれ
（Amazonリンクの予定地）
京都大学への数学(駿台大学入試完全対策シリーズ) 駿台文庫
最後の３冊目になりました！最後に紹介するのは駿台から出版されている参考書（どちらかというと過去問）になります。この本は駿台が実施している京大実践模試の過去問になります。過去に遡って５回分収録されていてなかなかのボリュームがあります。この本は特に解説が丁寧で、採点基準までもが記されていて独学にはもってこいの一冊。数学の他にも英語、国語、理科、地理歴史が発売されています！
筆者の感想
私はこの参考書を共通テスト〜二次試験本番までで取り組みました。京大の過去問を10年分もしくは25年分取り組み終わった人におすすめします。京大の過去問で見つけた課題をこの本で実践することができるので共通テスト〜二次試験本番の時期は時間があれば是非試して欲しいと思います。問題よりも解説に特に興味深いものが多いので是非手に取ってみてください！
（Amazonリンク予定地）
番外編 世界一わかりやすい京大の理系数学 著 池谷哲
名著かつ有名すぎる。大方の人が一度は取り組む参考書。もしかすると入試数学の掌握と同じ系統かも知れない。分野ごとではなく数学の問題の解き方を教えてくださる、一つの飛躍を感じられる参考書になります！
（Amazonリンク予定地）
新・物理入門〈増補改訂版〉 (駿台受験シリーズ) 駿台文庫 著 山本義隆
簡潔にこの参考書を紹介すると、どこが入門やねん！！という参考書でした。おそらく大学物理の入門にはちょうどいいのかも知れません。しかしながらこの参考書はただ漠然と公式を当てはめてとく物理から、公式の成り立ちや現象そのものを理解して「物理」に取り組めるようになります。そしてもう一つの特徴としてこの参考書では微分積分が多分に用いられています。（なんだか語呂がいい気がする。微分積分が多分）
筆者の感想
私はこの参考書を高校三年の春やすみから使い始めました。それまでは学校で配られる教材を用いて学習していたのですが少し物足りなくなってこの参考書を手に取った次第です微分積分を用いた公式や現象の解説をしてくださっているので、より感覚的に理解しやすいように感じました。
一度手に取ってみてみてください！！
(Amazonリンク予定地)
新・物理入門問題演習〈改訂版〉 (駿台受験シリーズ)駿台文庫 著 山本義隆
二冊目は一冊目の問題集版です。この問題集の面白いところは記述問題まであるところ！基本→応用→記述問題の構成になっていて、基本問題からなかなかタフな問題もあるのですが無秩序に難しいというわけではなく、整理してうんと考えることができる問題が多く掲載されていると感じました。
筆者の感想
私は新物理入門と並行して解き進めて行きました。やはり同じ方がこの２冊の参考書を書かれているので非常に相性が良く、新物理入門で学んだ知識や知恵を新物理入門問題演習で試すことができたので非常に成長を感じました。2冊ともやってみるのをおすすめします！
まとめ
いかがだったでしょうか！
本日は
- テーマ別演習① 入試数学の掌握 総論編
- 数学Ⅰ＋A＋Ⅱ＋B＋ベクトル 上級問題精講
- 京都大学への数学(駿台大学入試完全対策シリーズ)
- 新・物理入門〈増補改訂版〉 (駿台受験シリーズ)
- 新・物理入門問題演習〈改訂版〉 (駿台受験シリーズ)
の５冊と
世界一わかりやすい京大の理系数学
そして参考に 基幹講座 物理学 力学
を紹介させてもらいました！ご興味があれば書店でも一度手に取ってみてくださいね〜
いかがだったでしょうか。高校物理ではあまり取り組むことがない微分積分を用いる物理はより感覚的に、直感的にわかりやすい（個人差はある）と思いました。私も微積物理を高校生の時に少しばかり齧ってみてうまく行きました。
そして
何よりも、めっちゃやる気出る
割とやる気が大事だったりします。
ご覧いただきありがとうございました！
こんな感じの記事をぼちぼち書いています。よかったらまたみにきてくださいね〜☺️
かんたろう
photo:ぱくたそ
コメント